1. 💡최대 유량이란?
그래프에서 두 정점 사이에 얼마나 많은 유량(flow)을 보낼 수 있는지 계산하는 알고리즘을 네트워크 유량(Network Flow) 혹은 최대 유량(Maximum Flow) 알고리즘이라고 한다.
아래 용어들은 최대 유량 알고리즘을 이해하는데 도움이 되므로, 미리 짚고 넘어가자.
용량(Capacity)
Capacity[u][v]는 정점 u에서 v로 가는 간선의 용량이다.
유량(Flow)
flow[u][v]는 정점 u에서 v로의 간선(파이프)에 실제로 흐르는 유량을 의미한다.
잔여 용량(Residual Capacity)
간선의 용량과 유량의 차이를 의미한다.
ResidualCapacity[u][v] = Capacity[u][v] - flow[u][v]
즉, 해당 간선에 추가적으로 더 흘려 보낼 수 있는 유량이다.
소스(source)
모든 유량이 시작되는 정점으로 모든 유량은 source에서 출발하여, sink로 흐르게 된다.
싱크(sink)
모든 유량이 도착하는 정점이 싱크이다.
즉,최대 유량 알고리즘은 source에서 sink로 흐를 수 있는 최대 유량을 계산한다.
이러한 최대 유량 문제를 해결하기 위해서는, 포드 풀커슨 알고리즘을 활용해야한다.
1.1. ❓포드-풀커슨 알고리즘(Ford-Fulkerson Algorithm) 이란?
해당 알고리즘에는 역방향 유령 간선이라는 다소 생소한 개념이 등장하기 때문에,
먼저 이해하기 쉽게 그림으로 설명해보겠다.

먼저 위와 같은 그래프가 존재한다고 생각해보자.
이때 우리는 source에서 sink로 흐르는 최대 유량을 구하고 싶다.

먼저 직관적으로 봤을 때는, 해당 그래프는 다음과 같이 2개의 경로와 2의 최대유량을 가진다는 것을 알 수 있다.
하지만 만약 프로그램이 위와 같이 source -> a -> b -> sink의 경로를 먼저 탐색하게 된다면,

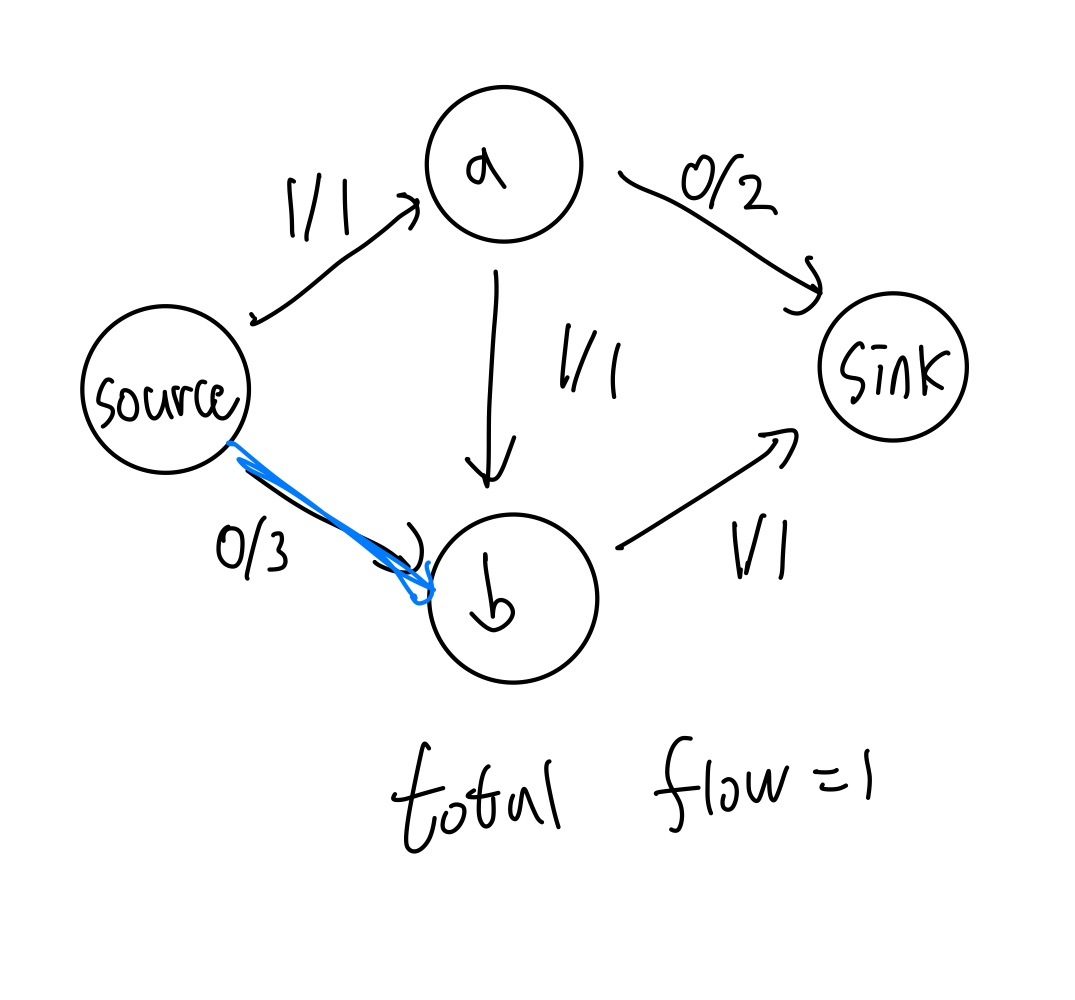
다음과 같이 source -> b -> sink 경로를 탐색하는 과정에서 이미 b -> sink 간선에서 capacity만큼의 flow가 흐르고 있기 때문에 추가로 유량이 흐르지 못하고, total flow가 1이 되면서 프로그램이 끝나게 되어버린다.
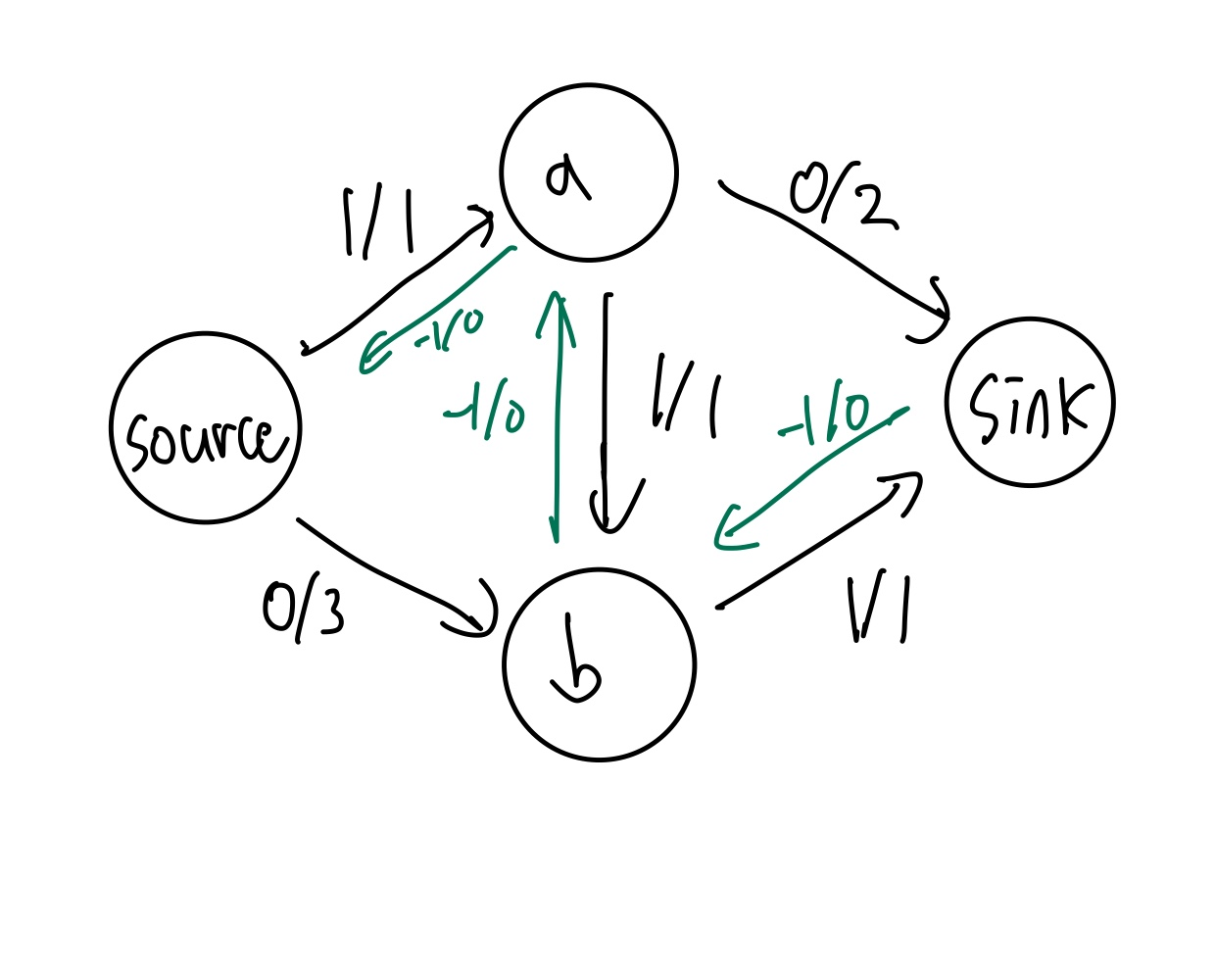
그래서 포드 풀커슨은 위와 같이 음수 유량을 가지는, 유령 간선을 생성하는 방법을 고안해냈다.
source -> a -> b -> sink로 향하는 경로에 유량을 채워나갈때, 채운 유량만큼을 음수로 가지고 capacity가 0인 유령 간선을 생성하는 것이다.
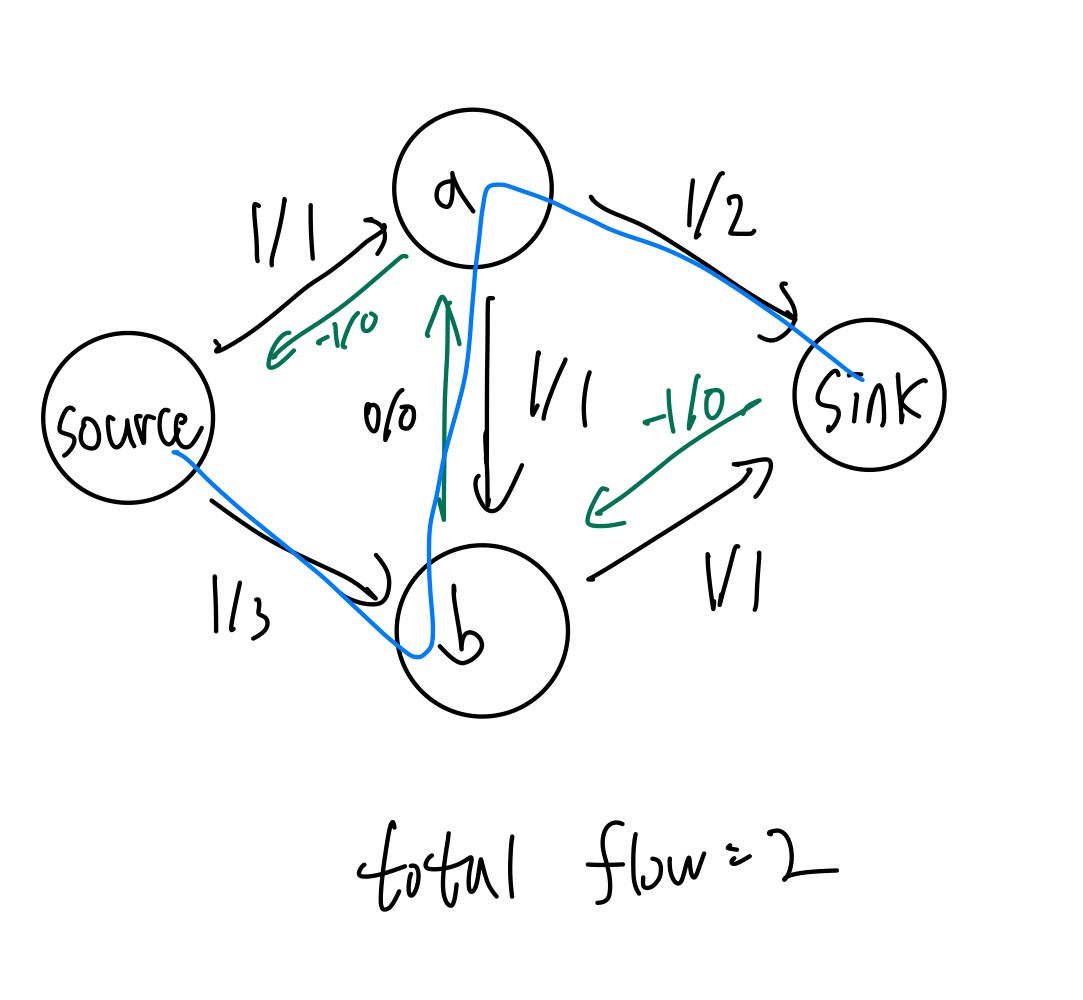
그럴 경우 위 그림과 같이 source -> b-> a-> sink로 향하는 경로가 생기게 되고, 결국 total flow는
기존에 우리가 생각한 최대 유량과 같은 2가 되게 된다.
사실 유령 간선을 사용하는 위와 같은 방법은 유량의 대칭성 ( f(u, v) == -f(v, u) ) 덕분에 가능한 유량의 상쇄라는 개념을 활용한 방법인데, 이를 증명하는 글은 다음 블로그에서 확인할 수 있다. (너무 deep하기 때문에 여기선 다루지 않겠다..)
1.2. ⚒️포드-풀커슨 알고리즘 정리
- Source에서 Sink로 가는 경로를 하나 찾는다. (증가 경로)
- 이 때, 경로에 포함된 모든 간선(파이프) 들은 flow 값(유량값)이 capacity(용량)을 넘을 수 없다.
- 만약 이미 flow값이 capacity값과 동일해진 간선의 경우는 지나갈 수 없는 경로가 된다.
- 해당 경로에서 보낼 수 있는 최대 유량값을 찾는다.
- 해당 경로의 최대 유량값은, 경로에 존재하는 모든 간선들의 가능한 유량값 (각 간선의 capacity - flow 값) 중 최솟값이다. (예를 들어 경로에 0/1과 1/3이 존재할때, 유량값으로 2를 흘려보내면 1/3은 3/3으로 만족이 되지만 0/1은 2/1가 되며 overflow가 일어나 불가능해진다. 따라서, 해당 경로에서 흘려보낼 수 있는 최대 유량값은 1이 된다.)
- 해당 경로에 찾아낸 최대 유량값을 실제로 흘려보낸다.
- 해당 경로에 존재하는 모든 간선 (flow[u][v]) 에 2번에서 구한 최대 유량값을 더해준다.
- ex) a - b - c - d 와 같은 경로라면,
- flow[a][b]+= flow,
- flow[b][c] += flow,
- flow[c][d] += flow 을 해준다.
- ex) a - b - c - d 와 같은 경로라면,
- 동시에 '유량의 대칭' 조건에 따라서, 역방향 간선 역시 2번에서 구한 최대 유량값을 음수값으로 흘려 보낸다.
- e.g) a - b - c - d 와 같은 경로라면,
- flow[b][a] -= flow,
- flow[c][b] -= flow,
- flow[d][c] -= flow 을 해준다.
- e.g) a - b - c - d 와 같은 경로라면,
- 해당 경로에 존재하는 모든 간선 (flow[u][v]) 에 2번에서 구한 최대 유량값을 더해준다.
- 1번에서 sink로 가는 경로를 찾지 못할때까지 1~3을 반복한다.
1.3. ❓에드몬드-카프 알고리즘(Edmonds-Karp Algorithm)이란?
포드 풀커슨 알고리즘의 시간복잡도를 최대한 줄이기 위해 포드 풀커슨 알고리즘을 BFS로 구현한 것을, 에드몬드-카프 알고리즘이라고 한다. 최대 유량을 구할 때에는 대부분 에드몬드 - 카프 알고리즘을 사용하게 된다.
다음은 오늘 풀면서 확인해 볼 문제인 백준 6086번이다.
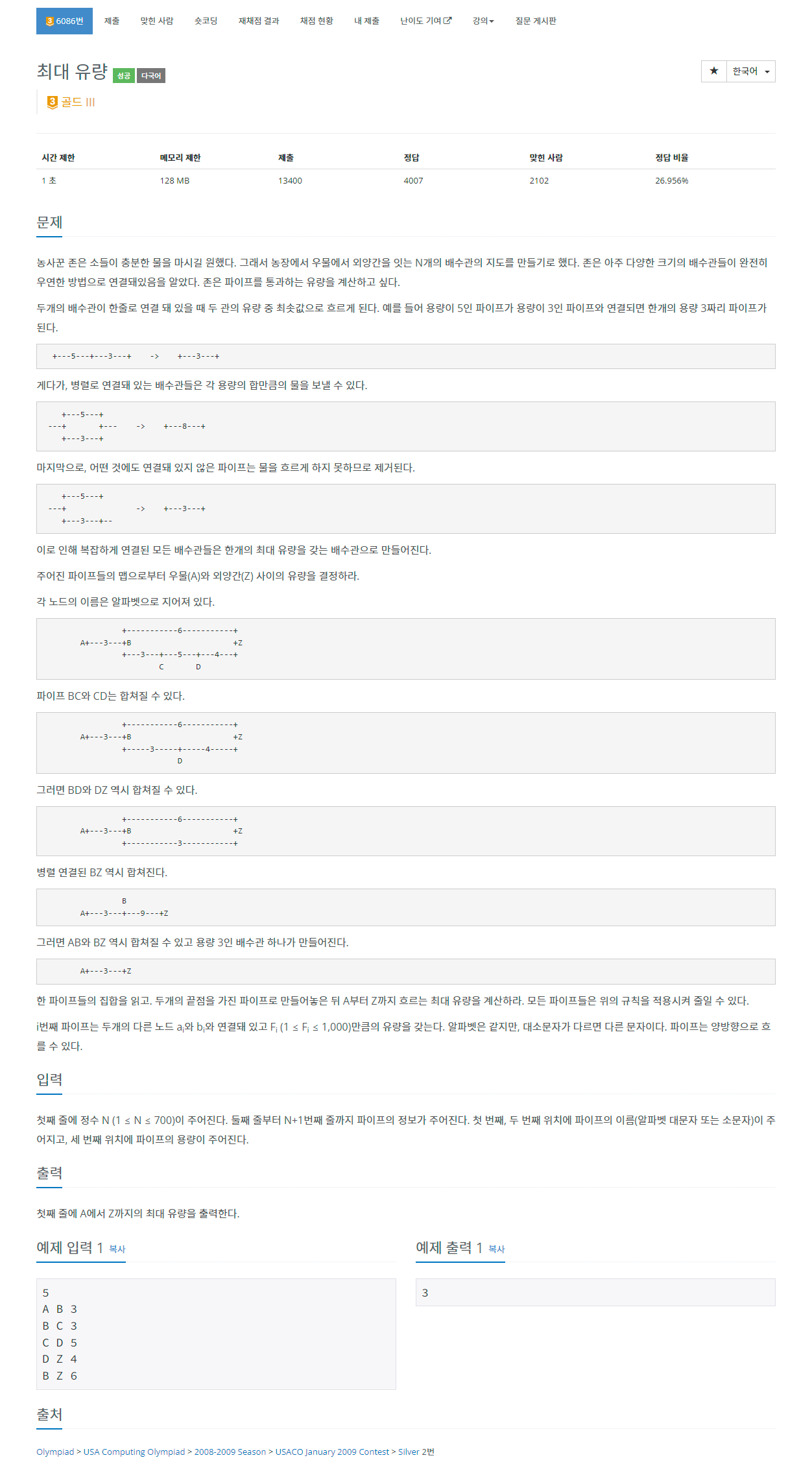
이 문제에서는 파이프들이 양방향으로 흐르기 때문에, 간선이 생성될 때 이미 양방향으로 생성이 될 것이고 따라서 유령 간선을 따로 생성할 필요가 없다. 하지만, 유량의 상쇄를 위해서 반대방향 간선의 flow를 현재 방향 간선에 흘려보낼 유량만큼 빼주는 과정은 반드시 포함하고 있어야 한다.
전체 코드를 보여주기 전, parent 배열에 대해 설명하자면,
해당 알고리즘을 BFS로 풀기 위해선 먼저 경로를 찾은 뒤, 해당 경로를 sink에서부터 거슬러 올라오며
모든 간선의 가능한 최대 유량중 최솟값을 찾고자 하기 때문에 역경로를 parent 배열에 저장하는 과정이 필요하다.
2. 📜CODE
<cpp />
#include <bits/stdc++.h>
using namespace std;
int n,sum;
int capacity[70][70];
int flow[70][70];
int source=1,sink=26;
int parent[70];
//A=65 Z=90 => A=1, Z=26
//z= 122
queue<int> Q;
void maxFlow(){
while(true){
for(int i=0; i<70; i++){
parent[i]=-1;
}
parent[source]=source;
Q.push(source);
while(!Q.empty()){
int cur=Q.front();
Q.pop();
for(int next=0; next<70; next++){
if(capacity[cur][next]>flow[cur][next] && parent[next]==-1){
Q.push(next);
parent[next]=cur;
if(next==sink) break;
}
}
}
if(parent[sink]==-1) break; // 더이상 sink로 가는 경로중 잔여용량이 남은게 존재하지 않을경우
int cur=sink;
int minflow=1010;
while(cur!=source){
int next=parent[cur];
int residualCapa=capacity[next][cur]-flow[next][cur];
if(residualCapa>0 &&(minflow>residualCapa)) {
minflow=residualCapa;
}
cur=parent[cur];
}
cur=sink;
while(cur!=source){
int next=parent[cur];
flow[next][cur]+=minflow;
flow[cur][next]-=minflow;
cur=parent[cur];
}
sum+=minflow;
}
}
int main(){
char Pnode,Nnode;
int capa;
cin>>n;
while(n--){
cin>>Pnode>>Nnode>>capa;
capacity[Pnode-64][Nnode-64]+=capa;
capacity[Nnode-64][Pnode-64]+=capa;
}
maxFlow();
cout<<sum;
return 0;
}
👀참고한 블로그
- https://gseok.gitbooks.io/algorithm/content/b124-d2b8-c6cc-d06c-d50c-b85c-c6b0/d3ec-b4dc-d480-cee4-c2a828-ford-fulkerson-c560-b4dc-baac-b4dc-ce74-d50428-edmonds-karp.html
- https://everenew.tistory.com/177
다음 풀어볼 문제
https://www.acmicpc.net/problem/11406
11406번: 책 구매하기 2
총 N명의 사람이 책을 구매하려고 한다. 각 사람은 1번부터 N번까지 번호가 매겨져 있고, 각 사람이 사려고하는 책의 개수는 A1, A2, ..., AN권이다. 이 책을 판매하는 온라인 서점은 총 M곳이 있다.각
www.acmicpc.net
'✏️PS' 카테고리의 다른 글
| [BOJ] - 1013 : Contact (0) | 2023.10.01 |
|---|---|
| [플로이드-워셜(Floyd-Warshall)] - BOJ_14938 : 서강그라운드 (0) | 2023.07.12 |
| [에라토스테네스의 체] - BOJ_1929 : 소수 구하기 (0) | 2023.05.19 |
| [느리게 갱신하는 세그먼트 트리] - BOJ_10999 : 구간합 구하기 2 (2) | 2023.05.18 |
| [세그먼트 트리] - BOJ_14427 : 수열과 쿼리 15 (0) | 2023.05.17 |

