2023.05.17 - [PS] - [세그먼트 트리] - BOJ_14427 : 수열과 쿼리
[세그먼트 트리] - BOJ_14427 : 수열과 쿼리
※본 포스팅은 이전 블로그에서 다시 이전해온 글로서 기존 작성일은 23.04.25 입니다. 요즘들어 PS를 하면서 느끼는게, 내가 이전에 공부하고 완전히 이해했던 자료구조 / 알고리즘들이 몇개월 지
kangmanjoo.tistory.com
지난 포스팅에 이어, 다시 한 번 세그먼트 트리로 돌아왔다.
세그먼트 트리는 특정 구간의 합, 곱, 최솟값, 최댓값을 찾을 때 일반적인 배열에서 찾을 때보다 훨씬 빠른 O(logN)의 시간복잡도를 가진다고 하였다. 그렇다면 세그 트리는 무적이고 나는 신인가?
물론 아니다. 세그트리에도 치명적인 단점이 존재하는데, 바로 값의 업데이트가 느리다는 것이다. 다음 경우를 한 번 살펴보자.
| INDEX | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| VALUE | 2 | 1 | 7 | 8 | 5 | 4 | 3 | 1 |
이전 포스팅의 배열을 재활용 하겠다.
해당 배열에서 index 3~7을 같은 값을 더해 업데이트 한다고 생각해보자..
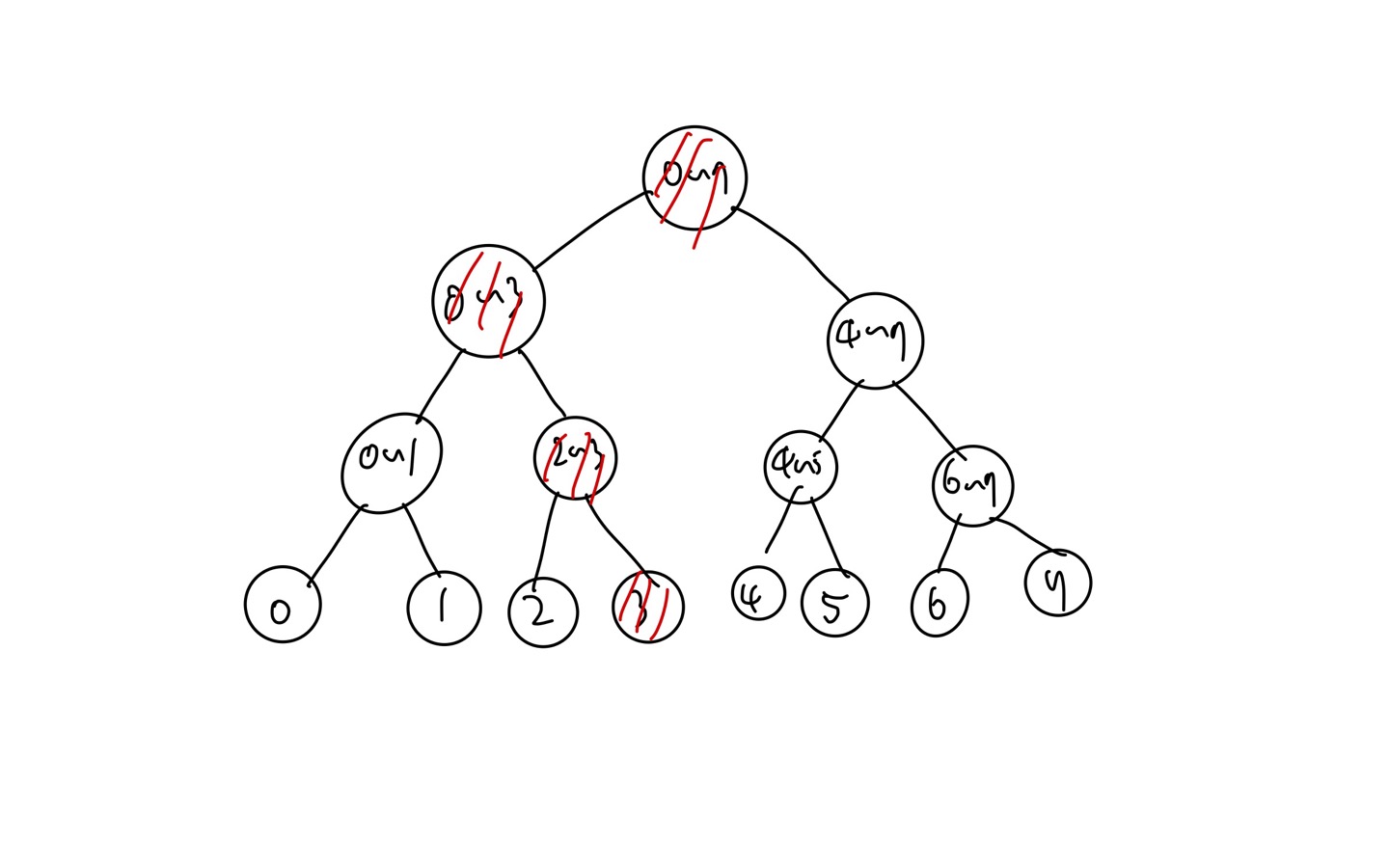
먼저 3과 3이 포함된 모든 구간 노드들을 업데이트 해줘야 할 것이다.
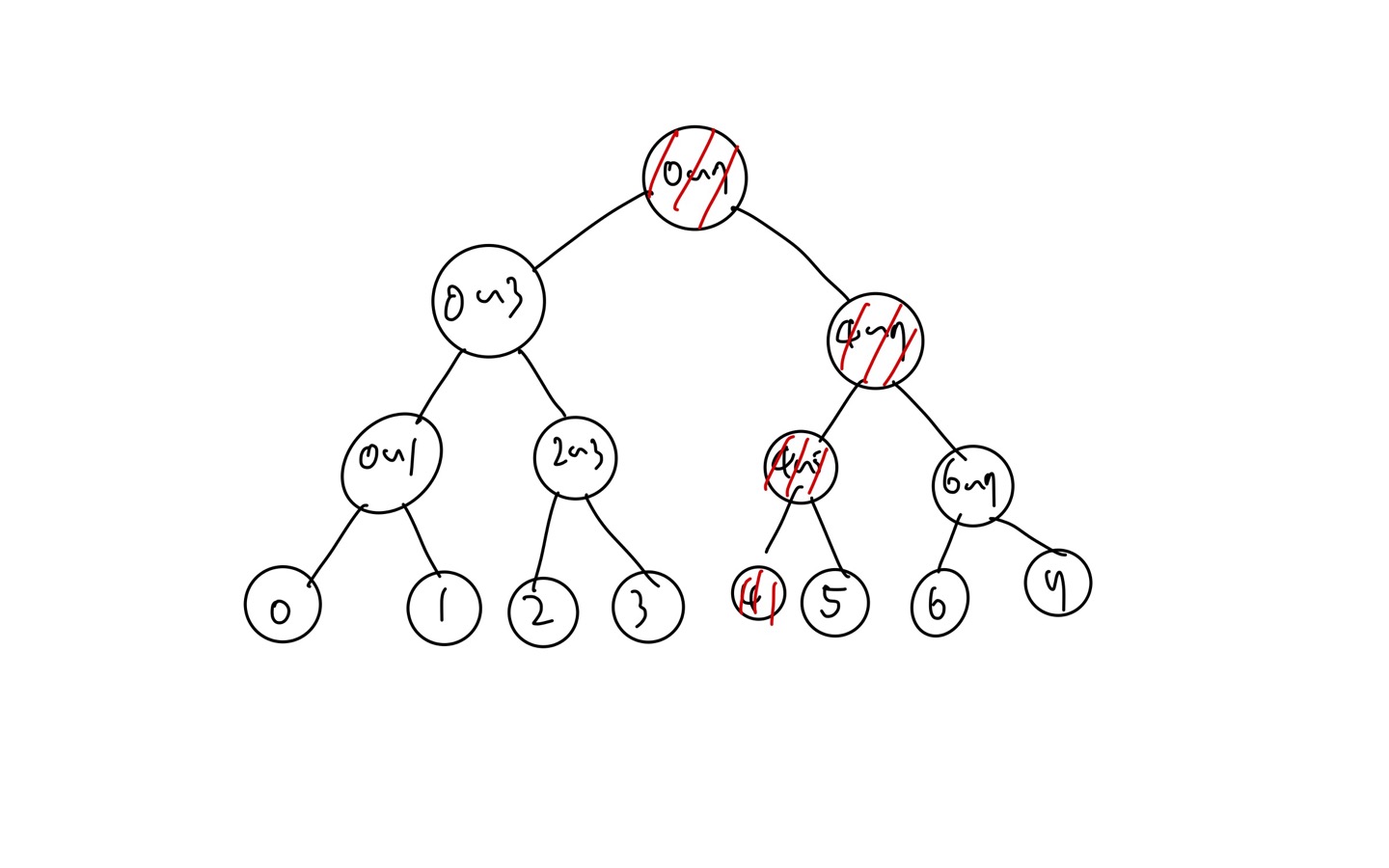
다음은 4와 4가 포함된 모든 구간을 업데이트 해줘야 할 것이고..
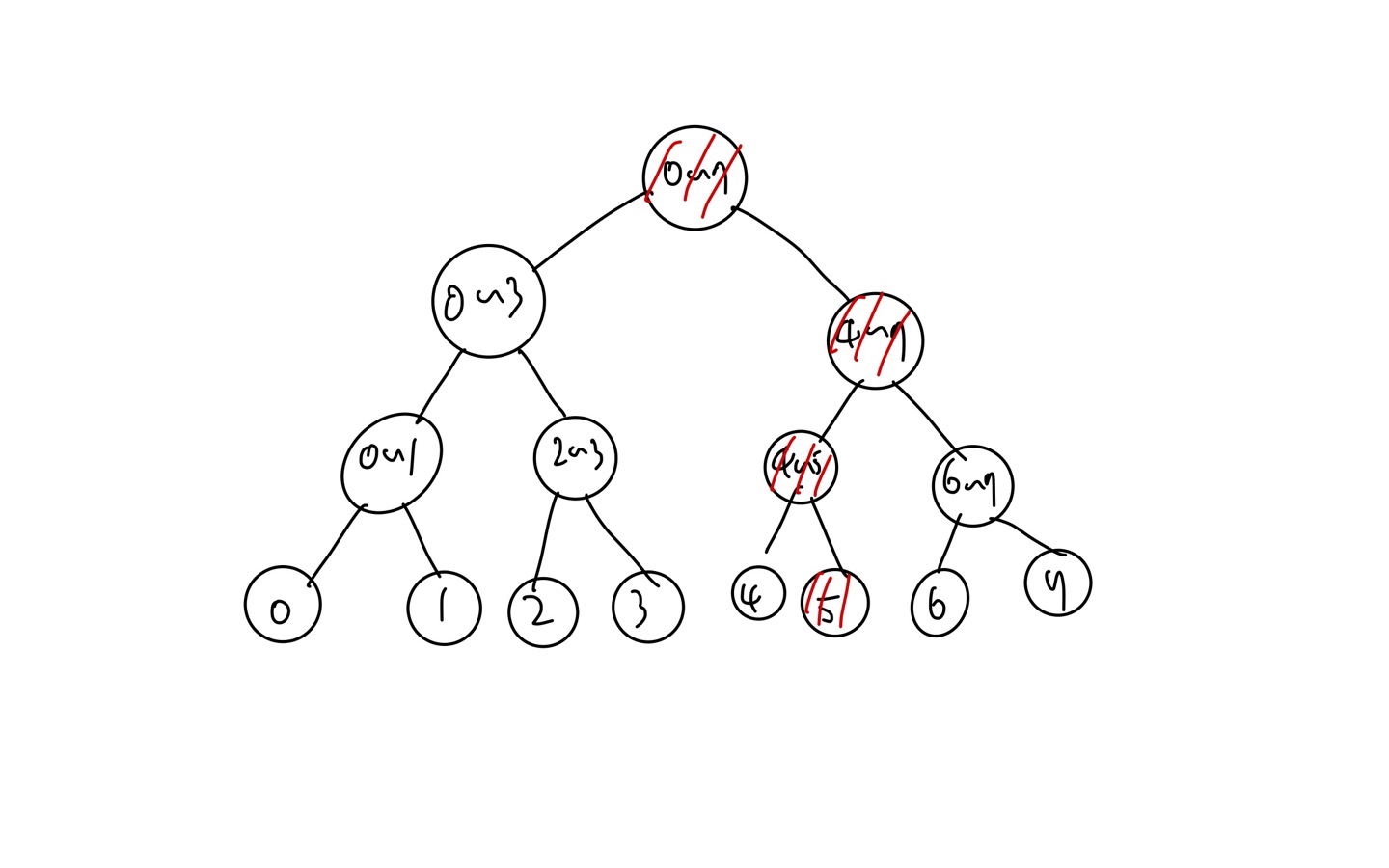
5와 5가 포함된 모든 구간도 업데이트 해줘야 할 것이다. 이를 6과 7도 같은 작업을 반복해주어야 한다.
그렇다면 이러한 구간 업데이트의 시간 복잡도는 얼마가 될 것인가? 각각의 업데이트가 O(logN)이므로, 바로 O(NlogN)이다!
거기에 쿼리가 M개가 주어진다면? 시간복잡도는 O(MNlogN)까지 기하급수적으로 올라갈 것이다.
그래서 과거의 천재들은 바로 _Lazy Propagation_이라는 방법을 떠올렸다.
느리게 갱신되는 세그먼트가 그래서 뭔데?
Lazy Propagation자료구조란, 세그먼트 트리에서 업데이트 해야하는 노드들을 바로 갱신하지 않고, 갱신시켜줘야 하는 값을 lazy라는 값으로서 해당 노드번호에 부여한다.
그리고, 해당 노드와 해당 노드의 하위 노드는 갱신하지 않고, lazy값을 가지고 있는다.
이후 해당 노드를 방문할 일이 생기면, lazy값을 해당 노드 값에 더해주며 갱신을 해 시간적 효율을 올리는 것이다.
위 예시로 lazy propagation을 실행하는 그림을 하나 그려보겠다.
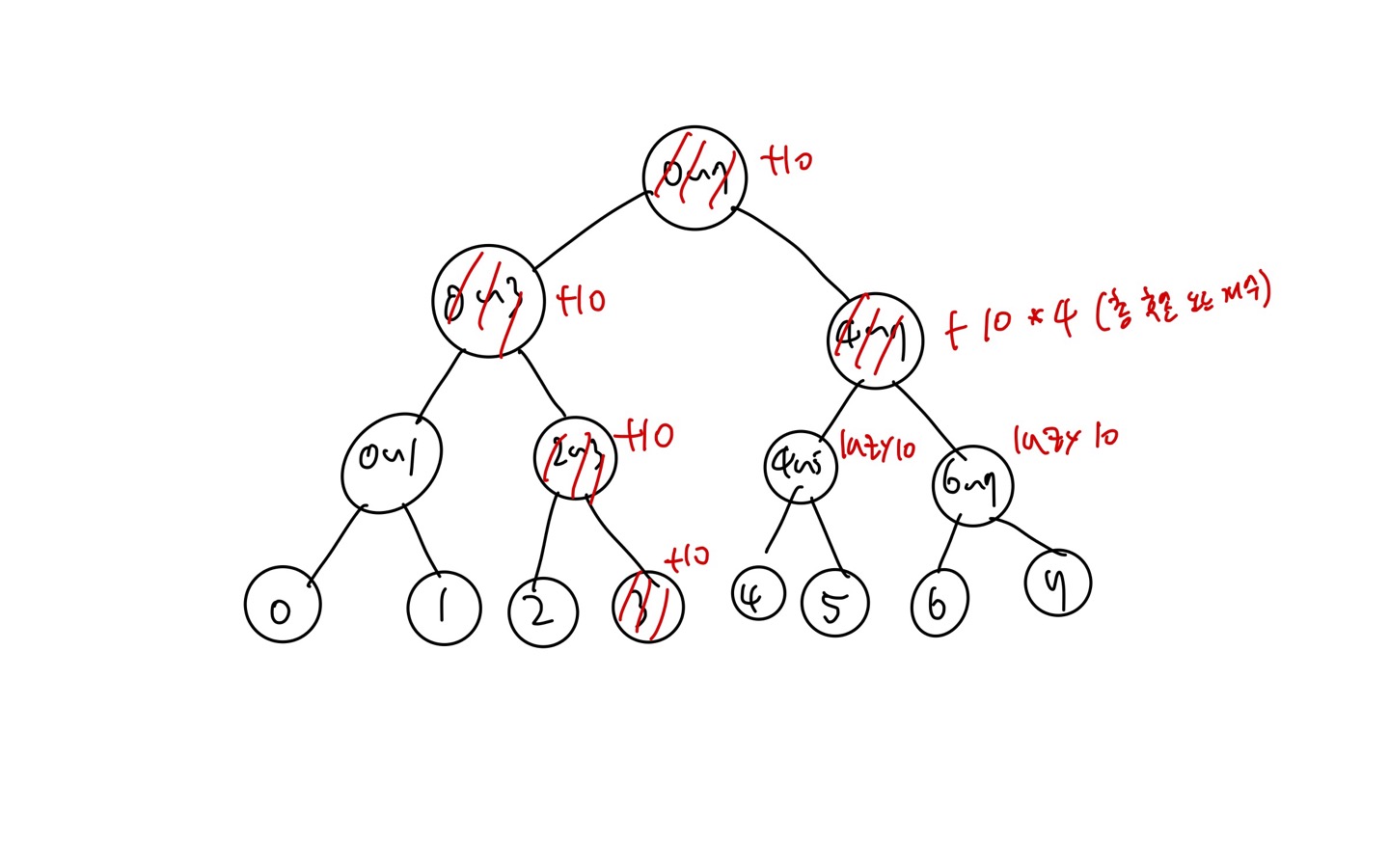
아까처럼 3 ~ 7범위에 +10이라는 계산을 해준다고 생각해보자.
3은 어쩔수 없이 leaf node까지 내려가며 갱신을 해준다.
하지만 4 ~ 7은?
4~7이라는 범위 노드가 존재하기에, 해당 노드를 갱신시키며 더 이상의 갱신을 하지 않는다.
why?
이후 노드들은 '현재의' 계산에서는 필요로 하지 않기 때문이다.
따라서 바로 자식노드에게, lazy값 +10을 부여하고, 갱신을 멈춘다.
그리고, 다음으로 해당 노드들을 방문할 일이 생기면, lazy값을 갱신해주는 것이다. 범위는 이해했을 것이라 생각하여 이제는 value값으로 설명을 해보겠다.
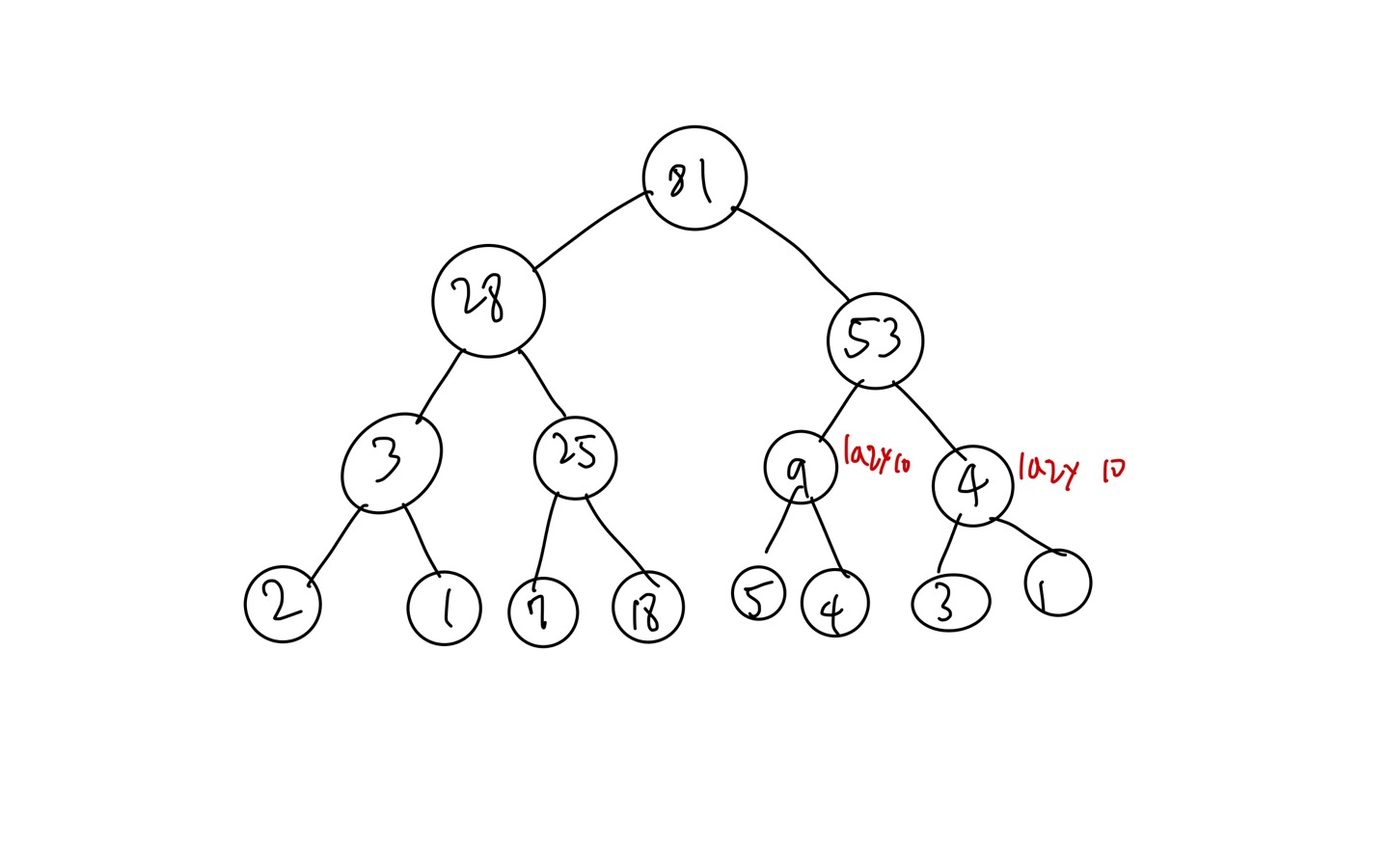
위 그림을 범위 대신 value로 나타낸 그림이다.
4 ~ 5 와 6 ~7 범위노드와 그 하위 노드들은 값이 갱신되는 대신, lazy값이 갱신된 모습을 확인해 볼 수 있다.
그렇다면 여기서, index 5~6에 +5 연산을 해보면 어떻게 될까?
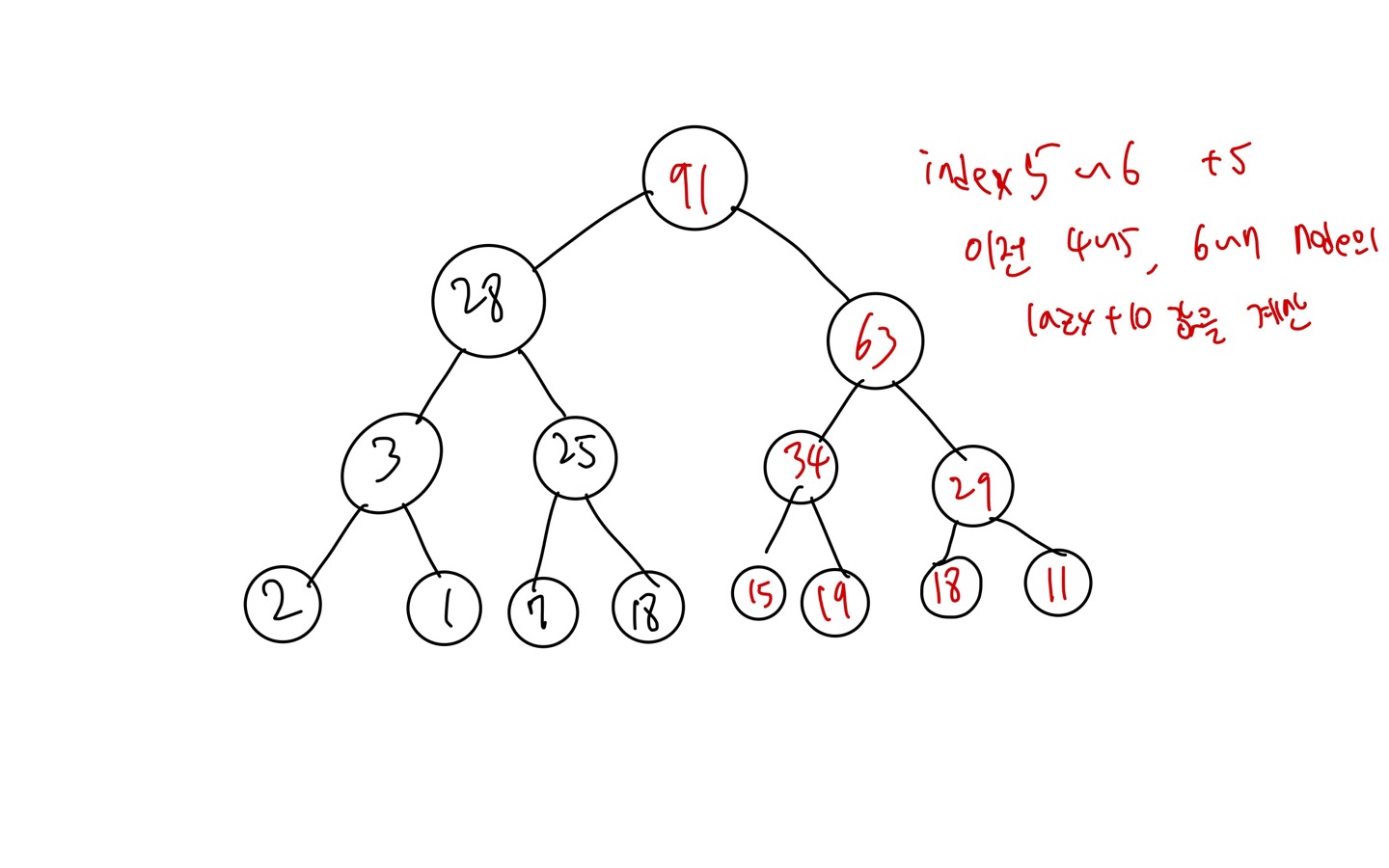
바로 위 그림과 같이 될 것이다. 새로운 연산을 해줌과 동시에,
lazy값이 걸려있던 범위노드들에게 lazy값을 계산해주는 것이다. 따라서, index5를 나타내던 leaf node인 13번 노드를 방문하기전에 범위 4~5를 나타내던 6번 노드를 지나쳤고, 바로 이 때 lazy값을 계산하는 것!
lazy propagation이 어느정도 이해가 되었다면, 이제 문제를 풀어보자.
https://www.acmicpc.net/problem/10999
10999번: 구간 합 구하기 2
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
다음은 백준 10999번 구간 합 구하기 2이다.
이 문제는 쿼리가 무수히 많기에, 느리게 갱신되는세그먼트 트리로 코드를 구성하지 않을 경우, 시간 초과에 걸리게 된다.
코드를 예시로 설명해보겠다.
void initSegTree(int node, int start, int end){
if(start==end){ //leafNode;
segTree[node]=arr[start];
return;
}
int mid=(start+end)/2;
initSegTree(node*2,start, mid);
initSegTree(node*2+1,mid+1, end);
segTree[node]=segTree[node*2]+segTree[node*2+1];
return;
}먼저 세그먼트 트리를 생성하는 코드이다.
이전 풀이에서는 이를 반복문으로 짰었는데, 이번에는
재귀문을 활용해봤다. 훨씬 쉽고 간단한듯해서 앞으로는
재귀를 활용하는게 좋아보인다.
void updateTree(int node,int left,int right,int start,int end,ll sumI){ //left,right=> node's range start,end=>find range
updateLazy(node, left, right);
if(left>end || right<start) return; //out of range
if(start<=left && right<=end){ //whole num in range
segTree[node]+=sumI*((ll)right-left+1);
if(left!=right){ //not leaf
lazy[node*2]+=sumI;
lazy[node*2+1]+=sumI;
}
return;
}
int mid=(left+right)/2;
updateTree(node*2,left,mid,start,end,sumI);
updateTree(node*2+1,mid+1,right,start,end,sumI);
segTree[node]=segTree[node * 2] + segTree[node * 2 + 1];
return;
}다음으로 트리를 업데이트 하는 함수이다.
7~9줄이 바로 내가 업데이트 하는 범위 내부의 범위 노드일경우,
해당 노드의 자식노드 갯수* 계산하는value를 해당 노드에 더해준뒤
자식노드들의 lazy값을 갱신해주는 코드이다.
함수 첫줄에서 lazy를 한 번 업데이트 해주는 이유는,
갱신을 위한 노드 탐색 중 lazy값이 붙어 있는 노드를 만난다면 우선 그 lazy값을 현재 노드에 반영해 주어야 하기 때문이다.
그렇지않으면, 이후 상위 노드들을 업데이트 해줄 때에 의도치 않은 오류가 발생할 수 있다.
if(start<=left && right<=end){ //whole num in range
segTree[node]+=sumI*((ll)right-left+1);
if(left!=right){ //not leaf
lazy[node*2]+=sumI;
lazy[node*2+1]+=sumI;
}
return;
}만약 갱신을 하지 않을경우, lazy값이 붙어 있는 노드가 새로 업데이트 하는 범위에 포함이 된다면 이곳에서 자신의 값을 갱신할 것이고,
segTree[node]=segTree[node * 2] + segTree[node * 2 + 1];해당 노드의 상위 노드는 위 재귀 코드에서 lazy가 갱신이 안되고, 새롭게 계산이 된 값을 받아들이게 될 것이기 때문이다. 즉, _오류_가 발생한다는 것!
void updateLazy(int node,int left, int right){
if(lazy[node]==0) return;
ll updateCost=lazy[node]*((ll)right-left+1); //long long type casting
segTree[node]+=updateCost;
if(left!=right){
lazy[node*2]+=lazy[node];
lazy[node*2+1]+=lazy[node];
}
lazy[node]=0;
return;
}마지막으로 가장 중요한 lazy값을 업데이트 해주는 함수이다.
정말 쉽다.
lazy값이 없다면 넘어가고, 있다면 해당 lazy값을 자식 노드 갯수를 기반으로 계산해준뒤,
자신이 leaf노드가 아니라면 해당 lazy값을 자신의 자식노드들에게도 물려주는것!
** 참쉽죠?**
전반적인 lazy propagation의 흐름을 파악했으니, 아래 전체코드를 보며 이해해보자.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,m,k;
ll segTree[4'040'004];
ll lazy[4'040'004];
ll arr[1'010'001];
void initSegTree(int node, int start, int end){
if(start==end){ //leafNode;
segTree[node]=arr[start];
return;
}
int mid=(start+end)/2;
initSegTree(node*2,start, mid);
initSegTree(node*2+1,mid+1, end);
segTree[node]=segTree[node*2]+segTree[node*2+1];
return;
}
void updateLazy(int node,int left, int right){
if(lazy[node]==0) return;
ll updateCost=lazy[node]*((ll)right-left+1); //long long type casting
segTree[node]+=updateCost;
if(left!=right){
lazy[node*2]+=lazy[node];
lazy[node*2+1]+=lazy[node];
}
lazy[node]=0;
return;
}
void updateTree(int node,int left,int right,int start,int end,ll sumI){ //left,right=> node's range start,end=>find range
updateLazy(node, left, right);
if(left>end || right<start) return; //out of range
if(start<=left && right<=end){ //whole num in range
segTree[node]+=sumI*((ll)right-left+1);
if(left!=right){ //not leaf
lazy[node*2]+=sumI;
lazy[node*2+1]+=sumI;
}
return;
}
int mid=(left+right)/2;
updateTree(node*2,left,mid,start,end,sumI);
updateTree(node*2+1,mid+1,right,start,end,sumI);
segTree[node]=segTree[node * 2] + segTree[node * 2 + 1];
return;
}
ll findSum(int node,int left,int right,int start,int end){
updateLazy(node,left,right);
if(left>end || right<start) return 0; //out of range
if(start<=left && right<=end){ //whole num in range
return segTree[node];
}
int mid=(left+right)/2;
return findSum(node*2,left,mid,start,end)+findSum(node*2+1,mid+1,right,start,end);
}
int main(){
cin.tie(nullptr)->ios::sync_with_stdio(false);
cin>>n>>m>>k;
ll val;
for(int i=1; i<=n; i++) cin>>arr[i];
initSegTree(1,1,n);
int query=m+k,q,a,b;
ll sumI;
while(query--){
cin>>q>>a>>b;
if(q==1){
cin>>sumI;
updateTree(1,1,n,a,b,sumI);
}
else if(q==2) {
cout<<findSum(1,1,n,a,b)<<'\n';
}
}
return 0;
}```
'✏️PS' 카테고리의 다른 글
| [최대 유량] BOJ_6086 : 최대 유량 (2) | 2023.05.25 |
|---|---|
| [에라토스테네스의 체] - BOJ_1929 : 소수 구하기 (0) | 2023.05.19 |
| [세그먼트 트리] - BOJ_14427 : 수열과 쿼리 15 (0) | 2023.05.17 |
| [머지 소트 트리] - BOJ_13537 : 수열과 쿼리 1 (0) | 2023.05.17 |
| [2-SAT] - BOJ_11280 : 2-SAT - 3 (1) | 2023.05.16 |

