※본 포스팅은 이전 블로그에서 다시 이전해온 글로서 기존 작성일은 23.04.25 입니다.
요즘들어 PS를 하면서 느끼는게, 내가 이전에 공부하고 완전히 이해했던 자료구조 / 알고리즘들이 몇개월 지나면 기억이 휘발되어 다시 포스팅들을 찾아보고 있는 내 모습이 너무 바보같았다.
그래서 이왕이면 내가 쓴 글을 보고 다시 떠올리자! 하는게 재습득하기도 제일 빠르고 나에게도 도움이 더 될 것같아, 이곳에 정리하기로 결정했다!
오늘 학습한 자료구조는 바로 세그먼트 트리
도대체 세그먼트 트리는 어디에서 활용이 되는 자료구조인가?
가장 대표적으로 활용이 되는 곳은, 바로 구간합을 구할때이다.
| INDEX | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| VALUE | 2 | 1 | 7 | 8 | 5 | 4 | 3 | 1 |
위와 같은 테이블이 있다고 하자.
이 배열에서 특정 구간의 합을 구한다고 생각을 해보자.
index 1~ 6을 구하려면 앞에서 부터 탐색하며 해당 구간의 value를 모두 더해주면 될 것이다. 매우 손쉬운 방법이지만, 데이터가 N개일 때의 시간복잡도는 O(N)으로 그리 만족스럽지 않은 속도일 것이다.
그렇다면 어떻게 더 빠른 방법으로 구간합을 구할 수 있을까?
먼저 우리가 아는 기본적인 트리의 형태를 그려본다.
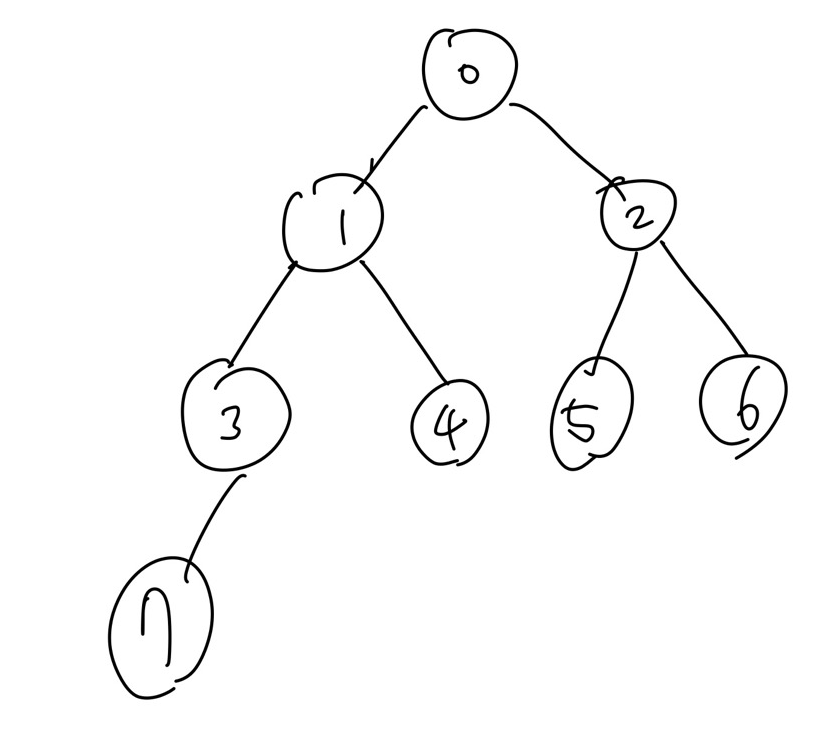
트리의 특성상 탐색을 한다면 시간복잡도는 O(logN)으로 기존보다 훨씬 많은 시간 단축을 할 수 있을 것이다.
그렇다면, 구간합은 어떻게 나타낸다는 것인가?
바로 다음과 같이 범위를 노드의 번호로 표현을 한다.
0번 노드는 index 0 ~ 7을 표현,
1번 노드는 index 0 ~ 4를 표현,
2번 노드는 index 5~7을 표현,
.
.
이런식으로 표현을 한다면, 어떠한 구간을 선택하든, 트리의 한 노드에 위치하기 때문에 탐색시간은 O(logN)이 된다.
매우 간단한 아이디어 아닌가!.. 싶지만, 떠올리기란 쉽지가 않으므로, 평소에 잘 학습해두자.
다음은 세그먼트 트리를 구현할 때의 몇가지 팁이다.
- 트리의 root 노드는 index 1로 표현한다. (탐색 코드를 짜기 훨씬 수월하다.)
- 어떠한 노드를 업데이트 할 경우, 해당 노드의 index구간이 위치하는 모든 트리의 index를 업데이트 해준다.
ex) 배열의 index3을 업데이트 할 경우, 트리에서 3이 포함된 모든 구간 노드들을 업데이트 (07, 04, 3~4, 3) - 트리의 크기를 초기화할때에는, 배열의 최대 범위의 4배만큼의 공간을 할당해준다. (N보다 큰 가장 가까운 수의 제곱수의 2배만큼의 공간을 필요로 하므로)

위 그림은 세그먼트 트리의 기본 구조이다.
이제 오늘의 문제를 풀어보자,
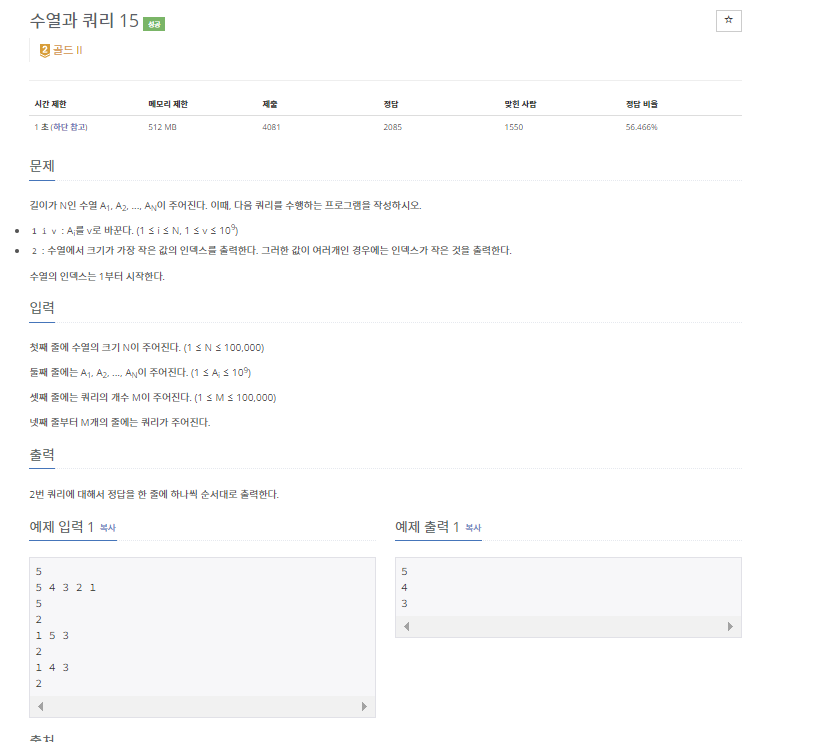
처음에 이 문제를 보았을 때는, 이게 대체 왜 세그먼트 트리지?
라는 의문이 있었다.
지금까지 구간합을 구할 때에만 세그먼트 트리 자료구조를 사용해왔던 나에게, 조금은 색다른 접근방식이었던 것이다. 이 문제에서는, 구간에서 가장 작은 value를 가진 index의 index 번호와 value값을 , pair 자료형으로 트리에 저장해주는 방식으로 세그먼트 트리를 응용해 줄 수 있다!
풀이와 코드 자체는 매우 간단하기 때문에, 구현은 쉬웠지만 이런식으로도 세그먼트 트리를 응용한다는 것을 배울 수 있어 굉장히 유익한 문제였다 :)
#include <bits/stdc++.h>
using namespace std;
int n,m,cost;
pair<int,int> arrTree[400'404];
void initTree(int cost,int curIdx){
int i=1;
int left=1; int right= n;
int treeIdx=1;
int mid;
if(arrTree[treeIdx].second==0||(arrTree[treeIdx].first>cost)){ //when treeIdx=1;
arrTree[treeIdx].first=cost;
arrTree[treeIdx].second=curIdx;
}
else if(arrTree[treeIdx].first==cost){
if(arrTree[treeIdx].second>curIdx){
arrTree[treeIdx].first=cost;
arrTree[treeIdx].second=curIdx;
}
}
while(left<right){
mid=(right+left)/2;
if(curIdx>mid){
left=mid+1;
treeIdx=treeIdx*2+1;
}
if(curIdx<=mid){
right=mid;
treeIdx*=2;
}
if(arrTree[treeIdx].second==0||(arrTree[treeIdx].first>cost)){ //first init or update minCost
arrTree[treeIdx].first=cost;
arrTree[treeIdx].second=curIdx;
}
else if(arrTree[treeIdx].first==cost){
if(arrTree[treeIdx].second>curIdx){
arrTree[treeIdx].first=cost;
arrTree[treeIdx].second=curIdx;
}
}
}
return;
}
void change(int curIdx, int newCost){
int treeIdx=1,mid,left=1,right=n;
while(left<right){
mid=(right+left)/2;
if(curIdx>mid){
left=mid+1;
treeIdx=treeIdx*2+1;
}
if(curIdx<=mid){
right=mid;
treeIdx*=2;
}
}
arrTree[treeIdx].first=newCost;
while(treeIdx){
treeIdx/=2;
if(arrTree[treeIdx*2].first>arrTree[treeIdx*2+1].first){
arrTree[treeIdx].first=arrTree[treeIdx*2+1].first;
arrTree[treeIdx].second=arrTree[treeIdx*2+1].second;
}
else{
arrTree[treeIdx].first=arrTree[treeIdx*2].first;
arrTree[treeIdx].second=arrTree[treeIdx*2].second;
}
}
}
void solve(){
cout<<arrTree[1].second<<'\n';
return;
}
int main(){
cin.tie(nullptr)->ios::sync_with_stdio;
fill(arrTree,arrTree+200002,pair<int,int>(0,0)); //pii init
cin>>n;
for(int idx=1; idx<=n; idx++) {
cin>>cost;
initTree(cost,idx);
}
cin>>m;
int q,a,b;
while(m--){
cin>>q;
if(q==1) {
cin>>a>>b;
change(a,b);
}
else solve();
}
return 0;
}'✏️PS' 카테고리의 다른 글
| [에라토스테네스의 체] - BOJ_1929 : 소수 구하기 (0) | 2023.05.19 |
|---|---|
| [느리게 갱신하는 세그먼트 트리] - BOJ_10999 : 구간합 구하기 2 (2) | 2023.05.18 |
| [머지 소트 트리] - BOJ_13537 : 수열과 쿼리 1 (0) | 2023.05.17 |
| [2-SAT] - BOJ_11280 : 2-SAT - 3 (1) | 2023.05.16 |
| [강한 연결 요소 SCC] - BOJ_2150 : Strongly Connected Component (1) | 2023.05.15 |

