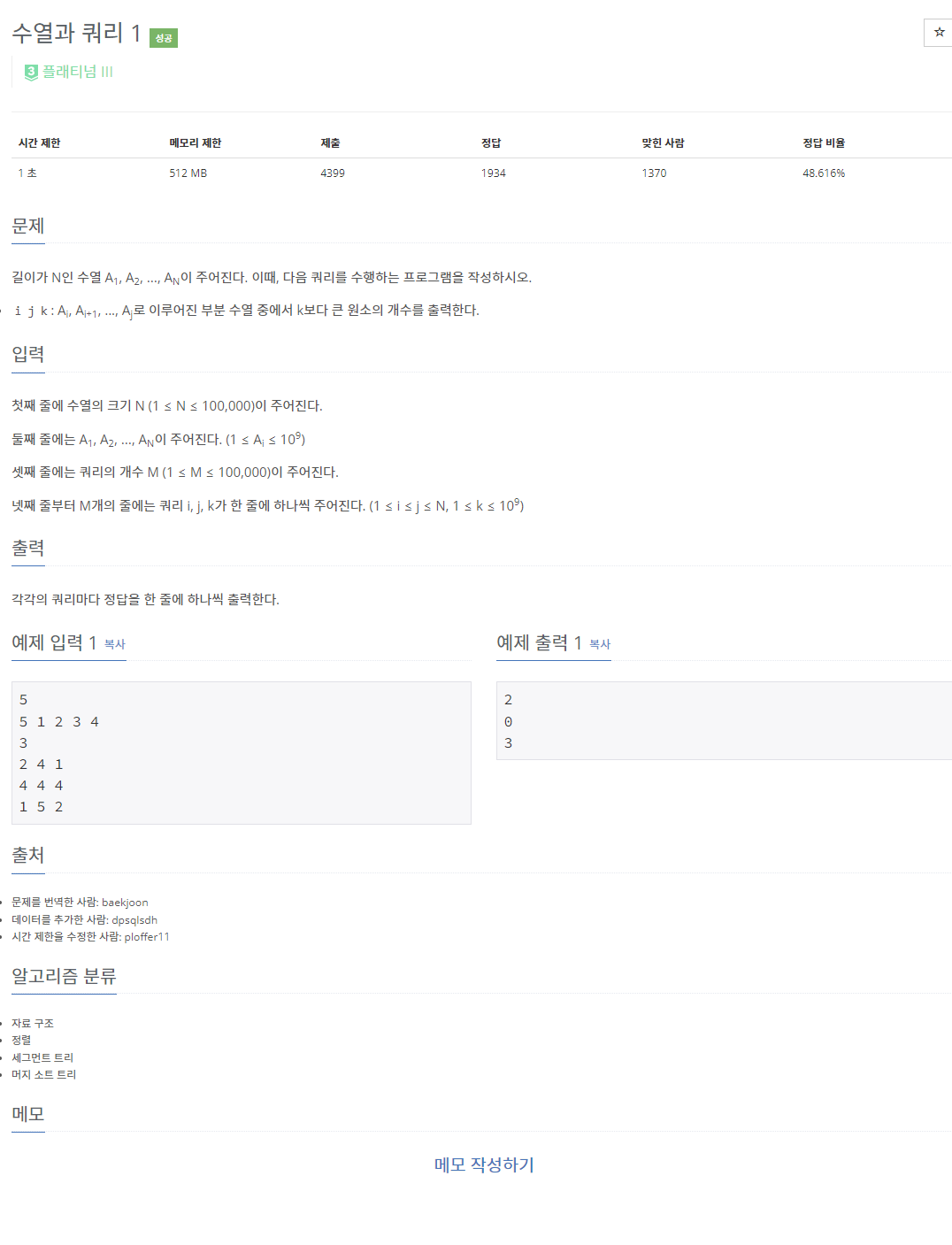
첫 플래티넘 3 솔브다 !!
세그먼트 트리를 활용하는 자료구조 중 재밌는게 없나 찾던 중,
머지 소트 트리라는 이름만 들어도 흥미로운 태그를 찾았다.
심지어 수열과 쿼리 '1' 이라니 안풀 수가 없잖아 !
❓머지 소트 트리(Merge Sort Tree)란?
일반적인 세그먼트 트리구조란, 해당 구간의 특징 (구간합이든, 최솟값이든.. 등등)을 각 범위를 지칭하는 노드에 저장을 한다. 머지 소트 트리도 마찬가지로, 특정 범위의 value들의 정렬 상태인 배열을 노드에 저장을 하는 구조이다.
사실 세그먼트 트리에 익숙하다면 크게 어렵지 않게 풀 수있다.
이번 문제에서는 개념을 묻는 느낌이라 갱신을 안해서 갱신부분은 고려를 안해보았는데, 이를 다루는 문제들도 풀어보면 좋을 듯싶다.
이 문제에서 한 번 실수했던 부분은 다음 코드이다.
if(start<=left && right<=end){
int size=segTree[node].size();
int idx=binary_search(node,0,size-1,k); //idx를 포함한 그 이후의 것들이 k보다 크다.
cnt+=size-idx;
}
k보다 큰값을 찾는 식인데, 이때 기껏 이분탐색으로 K보다 크기 시작하는 index를 구해놓고 for문을 돌리며 cnt값을 구하는 말도 안되는 실수를 해서 처음에 시간초과를 받았다.. (사실 처음에 각 value를 출력하는 줄 알고 for문으로 구현했었다.)
algorithm 헤더에 있는 upper_bound 함수를 사용하거나 이분탐색으로 k보다 큰 값의 index를 구해서 개수만 세주면 되는 문제.
👀upper_bound 사용예시
나는 upper_bound를 사용하지 않고 직접 binary_search를 공부 차원에서 구현했지만, 실제 코테를 볼때는 라이브러리 함수를 가져다 쓰는게 훨씬 유용하다.
upper_bound(arr.begin(), arr.end(), k) - arr.begin()다음과 같이 쓴다면, 이 함수는 반환값으로 k보다 큰 요소가 배열에서 처음 등장하는 index값을 반환해준다.
📜CODE
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int n,m,cnt;
int arr[100'001];
vector<int> segTree[400404];
int binary_search(int node,int left, int right, int val){
int mid= (left+right)/2;
if(left>right) return left;
else if(segTree[node][mid]>val){
right=mid-1;
return binary_search(node,left,right,val);
}
else{
left=mid+1;
return binary_search(node,left,right,val);
}
}
void initSeg(int node, int left, int right){
vector<int> v;
for(int i=left; i<=right; i++){
v.push_back(arr[i]);
}
sort(v.begin(), v.end());
for(auto &i: v){
segTree[node].push_back(i);
}
if(left==right) return;
initSeg(node*2, left, (left+right)/2);
initSeg(node*2+1, (left+right)/2+1, right);
return;
}
void findMST(int node, int left, int right, int start, int end, int k){
if(left>end || right<start) return;
if(start<=left && right<=end){
int size=segTree[node].size();
int idx=binary_search(node,0,size-1,k); //idx를 포함한 그 이후의 것들이 k보다 크다.
cnt+=size-idx;
}
else{
findMST(node*2, left, (left+right)/2, start, end, k);
findMST(node*2+1, (left+right)/2+1, right, start, end, k);
}
}
int main(){
cin.tie(0)->ios::sync_with_stdio(0);
cin>>n;
for(int i=1; i<=n; i++){
cin>>arr[i];
}
initSeg(1,1,n);
cin>>m;
int i,j,k;
while(m--){
cnt=0;
cin>>i>>j>>k;
findMST(1,1,n,i,j,k);
cout<<cnt<<'\n';
}
return 0;
}'✏️PS' 카테고리의 다른 글
| [느리게 갱신하는 세그먼트 트리] - BOJ_10999 : 구간합 구하기 2 (2) | 2023.05.18 |
|---|---|
| [세그먼트 트리] - BOJ_14427 : 수열과 쿼리 15 (0) | 2023.05.17 |
| [2-SAT] - BOJ_11280 : 2-SAT - 3 (1) | 2023.05.16 |
| [강한 연결 요소 SCC] - BOJ_2150 : Strongly Connected Component (1) | 2023.05.15 |
| [스프라그 그런디 정리] - BOJ_16895 : 님 게임 3 (0) | 2023.05.10 |

